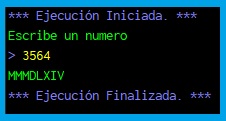
Hola amigos como están en esta ocasión realizamos un algoritmo para convertir numeros a romanos en pseint.
Haz clic aquí para suscribirte a mi canal
Bien como ya es costumbre vamos a explicar el funcionamiento de este algoritmo, lo primero que hacemos es ponerle un nombre en mi caso lo nombramos como:
Algoritmo detarea
Con la palabra reservada definir declaramos las variables, en este algoritmo utilizamos las variables a,c,d,u y n todas las declaramos de tipo entero.
Definir a,c,d,u,n Como Entero
Con la función escribir pedimos un número.
Escribir «Escribe un numero»
Este número lo almacenamos con la función leer en la variable n.
leer n
Ya que tenemos el número almacenado en la variable, entonces vamos separando las unidades.
Para obtener los millares dividimos el número entre mil con la función trunc y al resultado lo divinos entre 10 pero con la función mod para obtener únicamente el residuo, para las centenas, decenas y unidades hacemos lo mismo únicamente vamos cambiando el divisor.
Por ejemplo si aplicamos estas sentencias al número 3245 en la variable m se almacenaría el número 3, en la variable c el número 2, en la variable d el número 4 y el la variable u el número 5.
m = trunc(n/1000) mod 10
c = trunc(n/100) mod 10
d = trunc(n/10) mod 10
u = trunc(n/1) mod 10
Bien pues ya que tenemos los millares entonces evaluamos si la variable m es mayor a tres.
si m > 3 Entonces
Si la condición se cumple entonces significa que es un número superior a cuatro mil, por lo tanto mostramos un mensaje en pantalla indicando que el número no se pude calcular.
Ya que en los números romanos a partir del cuatro mil las reglas cambian.
Escribir «El numero no se puede calcular»
SiNo
Si la condición no se cumple entonces significa que el número que ingreso el usuario es menor a cuatro mil por lo tanto se puede calcular con este algoritmo.
Utilizamos la estructura según y comparamos si el número almacenado en la variable m es igual a 1,2 o 3, dependiendo el número mostramos en pantalla el número romano, este mensaje lo mostramos con a función sin saltar para que el número se muestre en una sola línea.
segun m hacer
1:
Escribir «M» Sin Saltar
2:
Escribir «MM» Sin Saltar
3:
Escribir «MMM» Sin Saltar
FinSegun
Para los centenas hacemos lo mismo que con los millares utilizamos la estructura según, y pues según el caso si el numero almacenado en la variable c es un numero entre 1 y 9 entonces mostramos el numero romano con la función sin saltar, como ya mencionaba para que se vaya uniendo en una sola sentencia los millares, y las centenas.
segun c hacer
1:
Escribir «C» Sin Saltar
2:
Escribir «CC» Sin Saltar
3:
Escribir «CCC» Sin Saltar
4:
Escribir «CD» Sin Saltar
5:
Escribir «D» Sin Saltar
6:
Escribir «DC» Sin Saltar
7:
Escribir «DCC» Sin Saltar
8:
Escribir «DCCC» Sin Saltar
9:
Escribir «CM» Sin Saltar
FinSegun
Nuevamente hacemos uso de la estructura según si el número almacenado en la variable d es un numero entre 1 y 9 entonces mostramos en pantalla el numero romano con la función sin saltar, ya con esto logramos imprimir en una sola línea los millares, las centenas y las decenas.
Segun d hacer
1:
Escribir «X» Sin Saltar
2:
Escribir «XX» Sin Saltar
3:
Escribir «XXX» Sin Saltar
4:
Escribir «XL» Sin Saltar
5:
Escribir «L» Sin Saltar
6:
Escribir «LX» Sin Saltar
7:
Escribir «LXX» Sin Saltar
8:
Escribir «LXXX» Sin Saltar
9:
Escribir «XC» Sin Saltar
FinSegun
Nuevamente utilizamos la estructura según, comparamos si en la variable u se encuentra un numero almacenando entre 1 y 9, según el caso imprimimos el numero romano correspondiente.
Segun u hacer
1:
Escribir «I»
2:
Escribir «II»
3:
Escribir «III»
4:
Escribir «IV»
5:
Escribir «V»
6:
Escribir «VI»
7:
Escribir «VII»
8:
Escribir «VIII»
9:
Escribir «IX»
FinSegun
FinSi
Finalmente cerramos las estructuras y finalizamos el algoritmo.
FinAlgoritmo
Algoritmo detarea Definir a,c,d,u,n Como Entero Escribir "Escribe un numero" leer n m = trunc(n/1000) mod 10 c = trunc(n/100) mod 10 d = trunc(n/10) mod 10 u = trunc(n/1) mod 10 si m > 3 Entonces Escribir "El numero no se puede calcular" SiNo segun m hacer 1: Escribir "M" Sin Saltar 2: Escribir "MM" Sin Saltar 3: Escribir "MMM" Sin Saltar FinSegun segun c hacer 1: Escribir "C" Sin Saltar 2: Escribir "CC" Sin Saltar 3: Escribir "CCC" Sin Saltar 4: Escribir "CD" Sin Saltar 5: Escribir "D" Sin Saltar 6: Escribir "DC" Sin Saltar 7: Escribir "DCC" Sin Saltar 8: Escribir "DCCC" Sin Saltar 9: Escribir "CM" Sin Saltar FinSegun Segun d hacer 1: Escribir "X" Sin Saltar 2: Escribir "XX" Sin Saltar 3: Escribir "XXX" Sin Saltar 4: Escribir "XL" Sin Saltar 5: Escribir "L" Sin Saltar 6: Escribir "LX" Sin Saltar 7: Escribir "LXX" Sin Saltar 8: Escribir "LXXX" Sin Saltar 9: Escribir "XC" Sin Saltar FinSegun Segun u hacer 1: Escribir "I" 2: Escribir "II" 3: Escribir "III" 4: Escribir "IV" 5: Escribir "V" 6: Escribir "VI" 7: Escribir "VII" 8: Escribir "VIII" 9: Escribir "IX" FinSegun FinSi FinAlgoritmo
Bien amigos esta es la solución de este algoritmo para convertir un numero decimal a romano te dejo el código, espero te guste y más que nada te pueda ser de utilidad un saludo y nos vemos en la próxima entrega.
me has ayudado mucho en todos mis algoritmos ..
muchas gracias 🙂
Que bueno que te han servido, un saludo