Se tienen dos matrices cuadradas (de 12 filas y 12 columnas cada una). Realice un algoritmo que lea los arreglos y que determine si la diagonal principal de la primera es igual a la diagonal principal de la segunda. (Diagonal principal es donde los subíndices I, J son iguales). Represente la solución mediante el diagrama de flujo y el pseudocódigo.
Realice un algoritmo que lea los arreglos y que determine si la diagonal principal de la primera es igual a la diagonal principal de la segunda
Haz clic aquí para suscribirte a mi canal
Como ya es costumbre, vamos a explicar el funcionamiento de este algoritmo, entonces lo primero que hacemos es ponerle un nombre, en mi caso le puse:
Algoritmo detarea
Declaramos las variables.
Definir f,c,x,matriz1,matriz2 Como Entero
Colocamos el tamaño a las matrices.
Dimension matriz1[12,12],matriz2[12,12]
Utilizamos dos ciclos anidados.
para f = 1 Hasta 12 Con Paso 1 Hacer
para c = 1 Hasta 12 Con Paso 1 Hacer
En cada bucle generamos un numero al azar entre 1 y 9, y lo ingresamos en la matriz 1.
matriz1(f,c) = azar(9) + 1
Nuevamente generamos un numero al azar entre 1 y 9, y lo ingresamos en la matriz 2.
matriz2(f,c) = azar(9) + 1
FinPara
FinPara
Inicializo la variable x con el numero 0.
x = 0
Nuevamente utilizamos dos ciclos anidados.
para f = 1 Hasta 12 Con Paso 1 Hacer
para c = 1 Hasta 12 Con Paso 1 Hacer
Con estos ciclos mostramos los elementos de la matriz 1.
Escribir matriz1(f,c),» » Sin Saltar
Evaluamos si la variable f es igual a la variable c.
si f == c Entonces
Si la condición se cumple quiere decir que estamos analizando un elemento de la diagonal principal.
Por lo tanto evaluamos si ambas matrices tienen el mismo número.
si matriz1(f,c) == matriz2(f,c) Entonces
Si la condición se cumple, entonces incrementamos la variable x en 1
x = x + 1
FinSi
FinSi
FinPara
Escribir » «
FinPara
Escribir «»
Nuevamente con dos ciclos anidados, mostramos los elementos de la matriz 2.
para f = 1 Hasta 12 Con Paso 1 Hacer
para c = 1 Hasta 12 Con Paso 1 Hacer
Escribir matriz2(f,c),» » Sin Saltar
FinPara
Escribir » «
FinPara
Finalmente si la variable x es igual a 12, quiere decir que las matrices tienen las diagonales iguales.
si x == 12 Entonces
Escribir «Las diagonales son iguales»
SiNo
Si la condición no se cumple, entonces quiere decir que las diagonales son diferentes.
Escribir «Las diagonales no son diferentes»
FinSi
FinAlgoritmo
Te comparto el Diagrama de flujo.
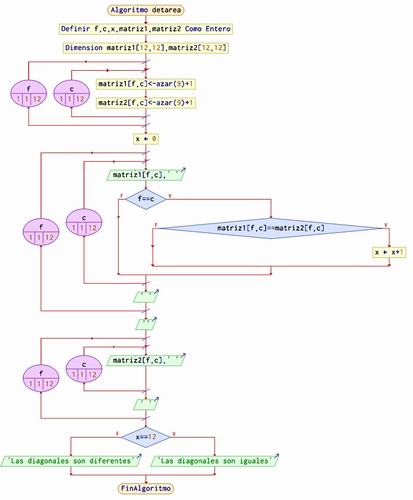
Bien amigos esta es la solución de este algoritmo, les comparto el código fuente, espero les guste y más que nada que les pueda ser de utilidad, un saludo y nos vemos en la próxima entrega.